

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
Cosserat continua with microstructure as models of media with non-mechanical properties
Modeling of media with various physical properties
Throughout the history of science many scientists have suggested the models of different physical phenomena and processes which are based on the conception of rotational character of motion of ether. Initially there were the conception of vortex motion of fluid (Descartes's philosophy) and the conception of rotation of elementary volume of solid (MacCullagh's ether), i. e. conceptions based on the models of continua possessing the translational degrees of freedom only. In the second half of XIX century the models in which the rotational motions are introduced as independent degrees of freedom (models by Maxwell, FitzGerald and Kelvin) have been suggested. The models of ether based on the translational degrees of freedom can not explain all facts known from experiments. The models of ether based on the rotational degrees of freedom, unfortunately, have not been developed. The reason is the fact that in the second half of XIX century the level of development of continuum mechanics made it impossible to describe 3D-continua with rotational degrees of freedom, and in the first decade of XX century scientists have almost completely refused the concept of the ether. Now, when the mechanics has come to perfectly new level of development nothing shall prevent us from giving a new substance to the idea of ether existence provided that we will use for this purpose advanced models of continuum mechanics.
 |
 |
 |
Modern concepts of atom and the simplest atom models used in physics and mechanics
 |
According to the concepts of modern physics atoms have a very complex internal structure, so that they can be in different energy states and possess the ability to radiate and absorb the energy quanta and elementary particles. These facts should be taken into account when the properties of a single atom or a molecule consisting of several atoms are studied. When modeling a medium which consists of billions of atoms many properties of atoms can be ignored or taken into account integrally, and it should be done so. Just as simulating the motion of crowds there is no need to take into account peculiarities of character, tastes and interests of each person. In statistical physics atoms are considered as mass points. Similarly, when modeling the crystal lattices very simple models of atoms are used, to be exact, atoms are assumed to be mass points or infinitesimal rigid bodies. With the help of long-wave approximation one can pass from the discrete model of a crystal lattice to the continuous model. If the atoms are modeled by mass points then one obtains the equations of classical momentless continuum. If the atoms are modeled by infinitesimal rigid bodies then one obtains the equations of the Cosserat continuum. In both cases one obtains a model possessing only mechanical properties. Suppose that after passing from a discrete model to continual theory we would like to have a continuum which possesses not only mechanical properties but also some physical properties described by the partial differential equations. We mean the continuous medium with electric, magnetic and thermal properties, which is able to radiate into the surrounding space both the acoustic waves and waves of another physical nature. In order to construct a discrete model of the medium possessing such properties we should consider atoms to be complex particles with internal structure and internal degrees of freedom rather than mass points or infinitesimal rigid bodies. |
 |
Use of complex particles as a basis of models of media with various physical properties
It is obvious that there are two types of particles with internal structure: the particles with internal translational degrees of freedom and the particles with internal rotational degrees of freedom. Particles of the first type are able to deform. Continua consisting of such particles possess two kinds of strains and stresses: the strains and stresses associated with the distance between the particles, and moreover strains of the particles themselves (the local strains) and the local stresses associated with the local strains. Such continua are called micromorphic continua. Particles of the second type are the quasi-rigid bodies which are also called the multi-spin particles or gyrostats. These particles consist of rotating rotors. The term "quasi-rigid body" means that the distances between any two rotors are kept unchanged under arbitrary motions of the quasi-rigid body but each rotor can rotate independently of rotations of other rotors. Continua consisting of such particles are called micropolar continua. The peculiarity of these continua is the fact that each them point has three translational and a few rotational degrees of freedom the number of which is determined by the number of rotors in multi-spin particles. All additional strains and stresses in micropolar continua are associated with the rotational degrees of freedom. In principle, both deformable particles and multi-spin ones can be used to model atoms and, consequently, both micromorphic and micropolar continua can be used to model the media possessing some non-mechanical properties. There are a number of arguments in favor of the multi-spin particles and micropolar continua:
Literature:
The basic idea of suggested method and some features of its implementation
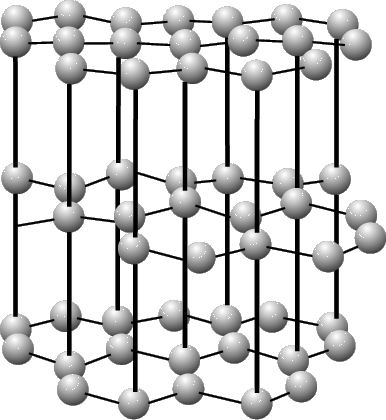
For modeling media with a combination of various physical properties we suggest to consider atoms as complex particles with internal rotational degrees of freedom. When a continuum theory is considered the radius-vector determining position of some point of the medium, in fact, determines position of the mass center of a representative volume which contains billions of atoms (see Figure). The continuous characteristics of rotational motions represent the quantities averaged over all atoms in the representative volume.

Continuum with microstructure: a) a representative volume in continuum; b) the representative volume on a large scale (atoms are visible); c) part of the representative volume on an even larger scale (the internal structure of atoms is visible). |
When choosing a specific particle to model atom the number of rotors inside the particle depends on the number of physical properties of the substance that should be taken into account. If only one non-mechanical property of the substance (for example, the ability to heat conduction) should be taken into account then one internal rotor is enough. Formally, transition from a multi-spin particle to the simpler model can be done using the following arguments. Let us consider a particle containing N internal rotors. If we are not interested in the rotation vectors and angular velocities of each rotor taken separately, and we are interested only in the quantities averaged over all rotors then the particle with N internal rotors can be replaced by a one-rotor gyrostat (see Figure). Let us assume that the dynamic characteristics of each rotor individually are not interested, but we need a particle that has exactly the same total dynamic characteristics (kinetic energy, momentum and angular momentum) as the multi-spin particle. In this case, a particle with N internal rotors can be replaced by the particle with three internal rotors (see Figure).
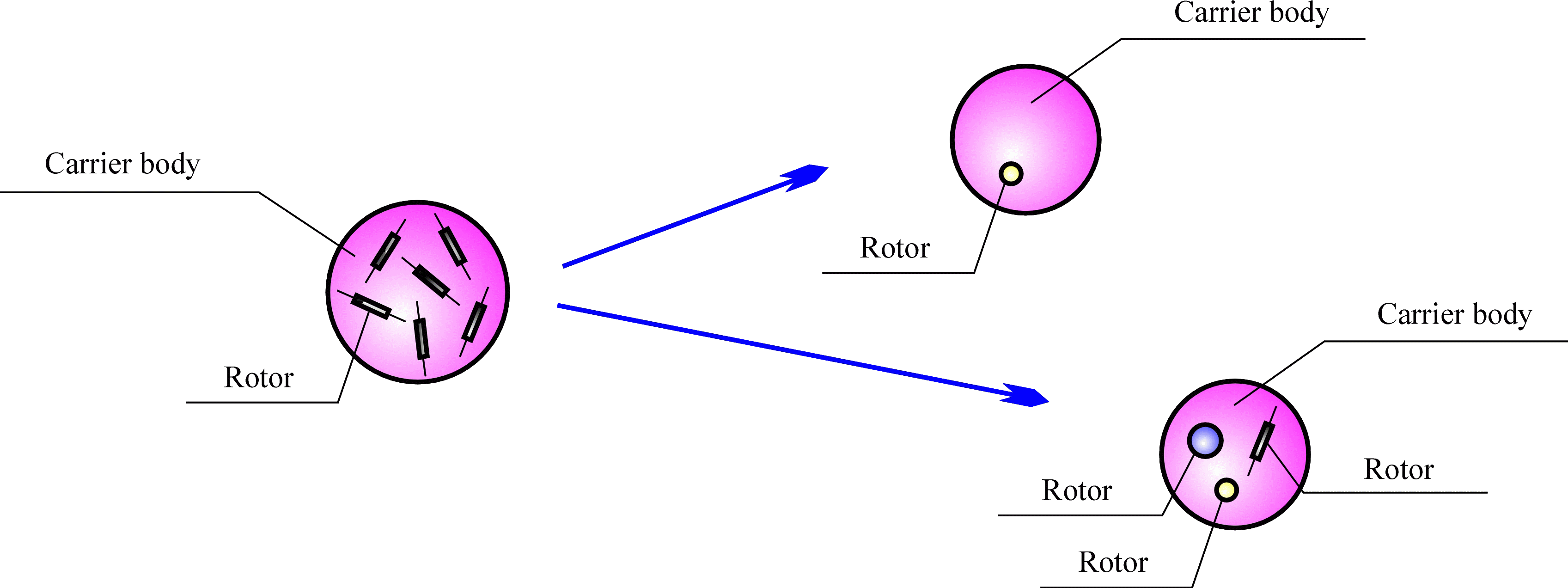
Multi-spin particle and its simplified models (one-rotor gyrostat and the particle with three internal rotors) |
When modeling the internal structure of atoms we suggest to use particles of special type which possess the property of dynamic relatedness of translational and rotational motions. This property is due to the presence of cross term in the expression for kinetic energy. Particles of this type were first introduced in consideration by P.A.Zhilin and later they were used to model the processes of thermal conductivity and internal damping. The use of these particles provides additional opportunities to account for the mutual influence of mechanical and non-mechanical processes.
To view PDF files you can download free version of Adobe Acrobat Reader.